梯度下降法及Matlab实现

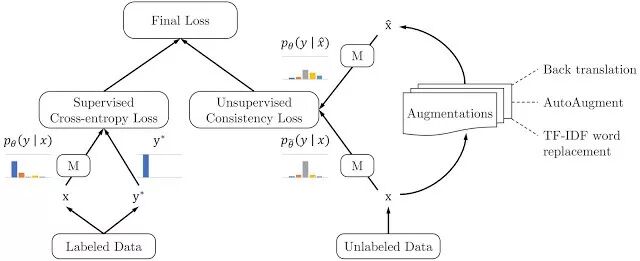
基本概念

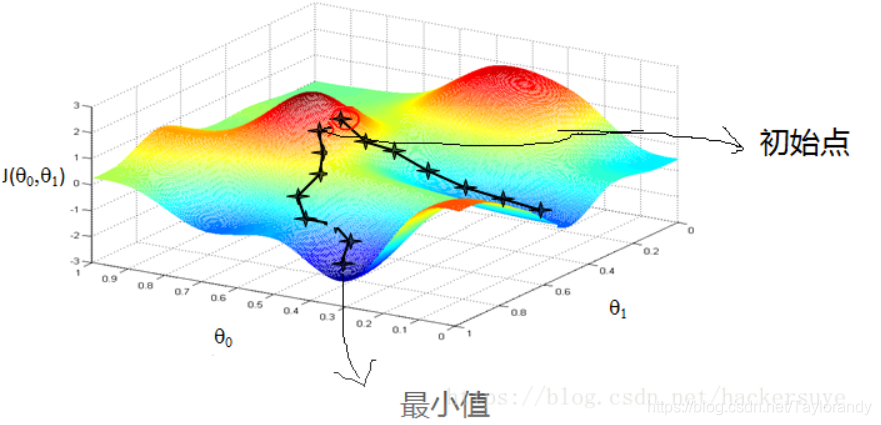
梯度下降法又被称为最速下降法( )，其理论基础是梯度的概念。梯度与方向导数的关系为：梯度的方向与取得最大方向导数值的方向一致，而梯度的模就是函数在该点的方向导数的最大值。梯度下降算法事实上是求多维函数的在某一点收敛的极小值，可以用这个算法迭代出在哪个点收敛，也是求最小二乘问题的一种方法。先在脑海中想象一下，你站在一座山上，怎么找到最快下山的方法，这时你当然会朝着最陡峭的方向前进，到达一个点后，再次朝着陡峭的方向下山，从而循环这些步骤，到达山脚。事实上，这也是梯度下降算法名字的由来，如图所示。

代码实现

梯度下降法的原理，本文不再描述，请参阅其它资料。

梯度下降法函数 =(f,x,e)，需要三个参数f、x和e,其中f为目标函数，x为初始点,e为终止误差。输出也为两个参数，k表示迭代的次数，ender表示找到的最低点。

steep.m

=(f,x,e)

%梯度下降法,f为目标函数（两变量x1和x2），x为初始点,如

syms x1 x2 m; %m为学习率

d=-

diff(f,x1);diff(f,x2)

;  %分别求x1和x2的偏导数，即下降的方向

flag=1;  %循环标志

k=0; %迭代次数

while(flag)

=subs(d,x1,x(1));      %将起始点代入，求得当次下降x1梯度值

=subs(,x2,x(2)); %将起始点代入，求得当次下降x2梯度值

nor=norm(); %范数

if(nor>=e)

=x+m*;            %改变初始点x的值

=subs(f,x1,(1));  %将改变后的x1和x2代入目标函数

=subs(,x2,(2));

h=diff(,m);  %对m求导，找出最佳学习率

=solve(h);   %求方程，得到当次m

x=x+*; %更新起始点x

k=k+1;

else

flag=0;