精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？

精确率(）是指在所有系统判定的“真”的样本中，确实是真的的占比，就是TP/(TP+FP)。

召回率（）是指在所有确实为真的样本中，被判为的“真”的占比，就是TP/(TP+FN)。

FPR（False Rate），又被称为“ of False Alarm”，就是所有确实为“假”的样本中，被误判真的样本，或者FP/(FP+TN)

在不谈具体任务的前提下谈指标就是耍流氓。

当然在谈具体任务之前，我们可以简单解释一下这些指标的概念。

假定有一个二分类问题，比如判定商品是否是假货。给系统一个样本，系统将会判断该样本为“真”（ ），或“假”（ ）。但是当然，系统的判断与真实判断（ /）是有误差的，将原本是真的判为真，就是TP（True ），原本真的判为假，就是FN（False ），原本假的判为真，就是FP（False ），原本假的判为假，就是TN（True ）。

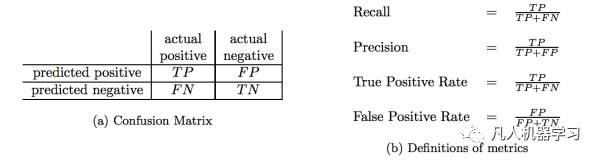
精确率(）是指在所有系统判定的“真”的样本中，确实是真的的占比，就是TP/(TP+FP)。

召回率（）是指在所有确实为真的样本中，被判为的“真”的占比，就是TP/(TP+FN)。

TPR（True Rate）的定义，跟一样。

FPR（False Rate），又被称为“ of False Alarm”，就是所有确实为“假”的样本中，被误判真的样本，或者FP/(FP+TN)

F1值是为了综合考量精确率和召回率而设计的一个指标，一般公式为取P和R的 mean:2**/(+)。

ROC= ，是TPR vs FPR的曲线；与之对应的是- Curve，展示的是 vs 的曲线。

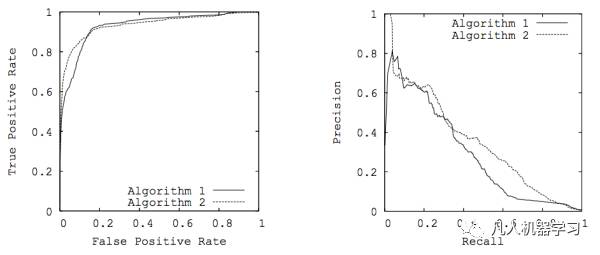
显而易见的，当TN=FN=0的时候，也就是我们将100%的样本都认为是“真”的，TPR=FPR=1：这就是我们“完全放水”的情形；反之，当TP=FP=0的时候，也就是我们将100%的样本都认为是“假”的时候，TPR=FPR=0，这就是“宁可错杀一万，不可放过一个”的情形。

我们在下图观察几个点。首先，FPR=0, TPR=1的那个点，可以推测FN=0, FP=0:一个错误都没有，所以是 。

中间这条红线，我们观察TPR=FPR，所以TP(FP+TN)=FP(TP+FN)，所以TP/FN = FP/TN：换言之，无论样本是真是假，我们将它们判为“真”或“假”的概率都相当，或者说，我们的猜测是完全随机的。

在红线上方，偏 的区域，我们认为是优于随机猜测。因为，在红线上的任意一点垂直向上的点，都有同样的FPR，但总是得到更高的TPR：在错误不变的情况下，我们的变高了。反之，在红线下方的点，都认为是劣于随机猜测。

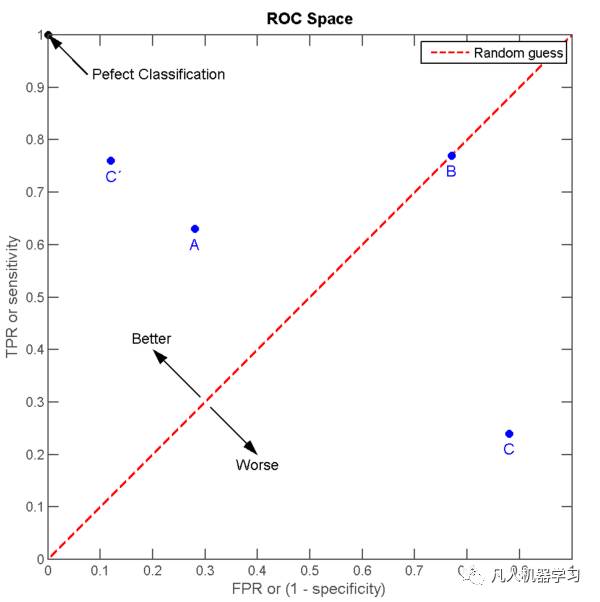
那么聪明的你一定想得到，ROC曲线下方所包围的面积越大，那么分类器的性能越优越。这个曲线下的面积，就叫做AUC（Area Under the Curve）。因为整个正方形的面积为1，所以0