层归一化与批量归一化区别

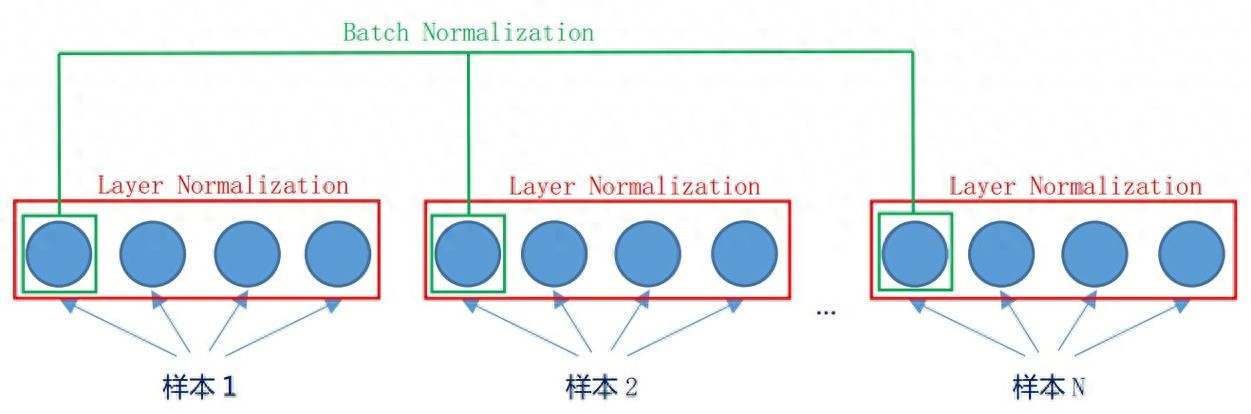
层归一化（LN）和批量归一化（BN）是深度学习中两种常用的归一化技术，虽然都旨在通过标准化数据分布提升模型训练稳定性，但它们的设计思路、适用场景和工作机制有本质区别。下面从多个维度详细对比：

一、核心原理：归一化的 “范围” 不同批量归一化（BN）：跨样本、同特征归一化层归一化（LN）：同样本、跨特征归一化二、计算方式对比

步骤

批量归一化（BN）

层归一化（LN）

1. 计算均值

对批次中所有样本的同一特征求平均

对单个样本的所有特征求平均

2. 计算方差

对批次中所有样本的同一特征求方差

对单个样本的所有特征求方差

3. 标准化公式

((x – mu_{text{batch, }}) / sqrt{sigma^2_{text{batch, }} + })

((x – mu_{text{, all }}) / sqrt{sigma^2_{text{, all }} + })

4. 缩放偏移

有可学习的缩放系数 (gamma) 和偏移量 (beta)

有可学习的缩放系数 (gamma) 和偏移量 (beta)

5. 训练 vs 推理

训练用批次统计量，推理用滑动平均统计量

训练和推理均用当前样本的统计量

三、关键差异点解析1. 对批次大小的依赖性2. 适用场景3. 推理阶段的处理4. 对数据分布的适应性四、直观类比：两种归一化的 “管理方式”

批量归一化（BN）

层归一化（LN）

像 “按科目分班”：把所有学生的数学成绩放一组，语文成绩放另一组，每组内单独标准化。

像 “按学生分班”：把每个学生的所有科目成绩放一组，每组内单独标准化。

依赖全班学生的数据来计算统计量

只依赖单个学生自己的数据来计算统计量

班级人数（批次大小）影响统计准确性

班级人数不影响，每个学生独立计算

五、总结：如何选择？

两者的核心目标一致 —— 通过标准化减轻 “内部协变量偏移”（数据分布随训练变化的问题），但因适用场景不同而形成了互补的技术路线。在 等现代架构中，LN 的优势使其成为标配，而 BN 仍在 CV 领域占据重要地位。