马尔可夫决策过程(MDP)：马尔可夫奖励(MRP) + 智能体动作因素

本文接前面文章：

根据上文我们已经得知，在随机过程的基础上

通俗讲，MRP与MDP的区别就类似随波逐流与水手划船的区别

在马尔可夫决策过程中，

(S是状态的集合)和

(R是奖励的集合)的每个可能的值出现的概率只取决于前一个状态

和前一个动作

(A是动作的集合)，并且与更早之前的状态和动作完全无关

换言之，当给定当前状态

(比如

)，以及当前采取的动作

(比如

)，那么下一个状态

出现的概率，可由状态转移概率矩阵表示如下

考虑到在当前状态和当前动作确定后，那么其对应的即时奖励则也确定了

，故的RL一书中，给的状态转移概率矩阵类似为

从而可得奖励函数即为

至于过程中采取什么样的动作就涉及到策略，策略函数可以表述为

函数(当然，这里的

跟圆周率没半毛钱关系)

通过上文，我们已经知道不同状态出现的概率不一样（比如今天是晴天，那明天是晴天，还是雨天、阴天不一定），同一状态下执行不同动作的概率也不一样（比如即便在天气预报预测明天大概率是天晴的情况下，你大概率不会带伞，但依然不排除你可能会防止突然下雨而带伞）

而有了动作这个因素之后，我们重新梳理下价值函数

首先，通过“状态价值函数”对当前状态进行评估

相当于从状态S出发遵循策略

能获得的期望回报

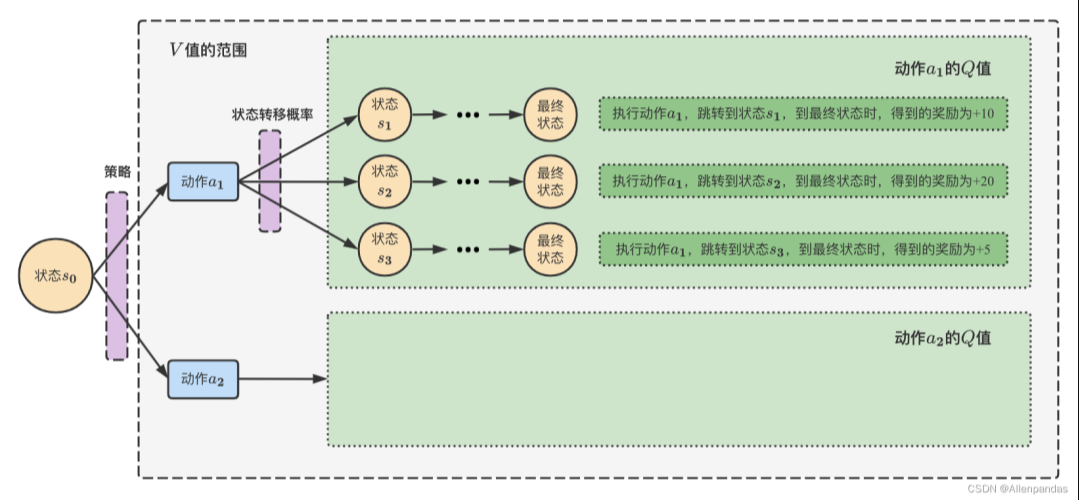
其次，通过“动作价值函数”对动作的评估

相当于对当前状态S依据策略

执行动作

得到的期望回报，这就是大名鼎鼎的Q函数，得到Q函数后，进入某个状态要采取的最优动作便可以通过Q函数得到

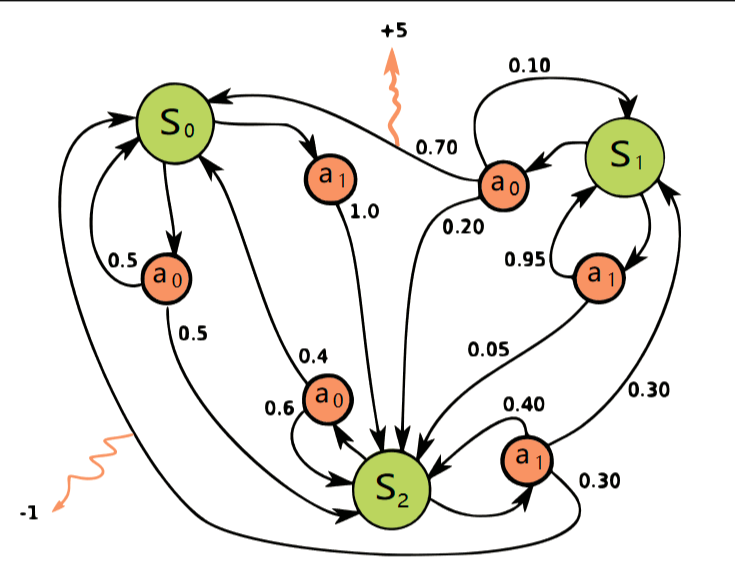
当有了策略、价值函数和模型3个组成部分后，就形成了一个马尔可夫决策过程（ ）。如下图所示，这个决策过程可视化了状态之间的转移以及采取的动作。

且通过状态转移概率分布，我们可以揭示状态价值函数和动作价值函数之间的联系了

我猜可能有读者会问怎么来的，简略推导如下

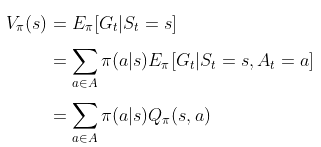
针对这个公式 大部分资料都会一带而过，但不排除会有不少读者问怎么来的，考虑到对于数学公式咱们不能想当然靠直觉的自认为，所以还是得一五一十的推导下

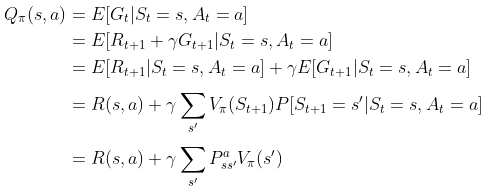
上述推导过程总共五个等式，其中，第三个等式到第四个等式依据的是

，至于第四个等式到第五个等式依据的是状态转移概率矩阵的定义

接下来，把上面

的计算结果互相代入，可得马尔可夫决策的贝尔曼方程

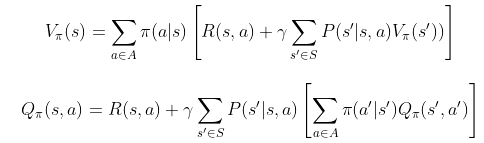
上述过程可用下图形象化表示(配图来自文献21)

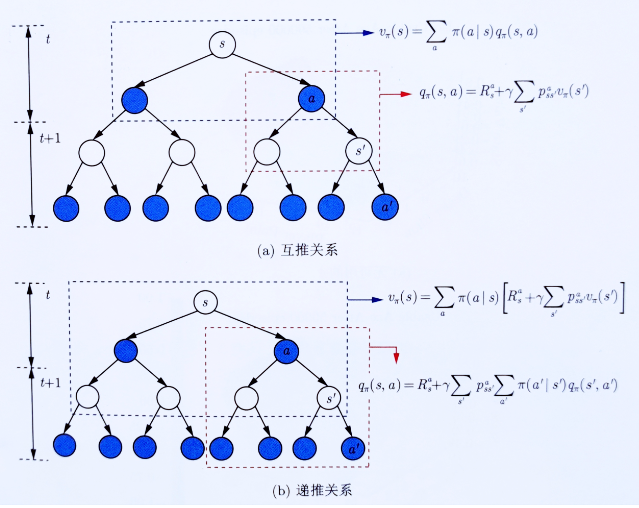
计算示例和更多细节待补充..

想在NLP领域更系统、深入提升的同学，我建议你看下【NLP高级小班 第十一期】

一次报名，答疑服务三年

考虑到市面上课程大都以讲技术、讲理论为主，鲜有真正带着学员一步步从头到尾实现企业级项目的高端课程，故我们让大厂技术专家手把手带你实战大厂项目。一方面，让大家更好的在职提升，另一方面，力求让每位同学都深刻理解NLP的各大模型、理论和应用。

第十一期，除了继续维持上一期的：

本期更对技术和项目阶段做了大力度改进：

面向群体： 本课程适合已经在做AI的进一步在职提升，比如在职上班族跳槽涨薪/升职加薪，采用严格筛选制（通过率不到1/3），需要具备一定的基础能力才能报名通过，故以下同学优先：

【NLP高级小班 第十一期】已开营，放5个免费试听名额，有意找苏苏老师（VX： ）或七月在线其他老师申请试听了解课程

      
（扫码联系苏苏老师）