教程 | 无监督学习中的两个非概率模型：稀疏编码与自编码器

参与：Smith

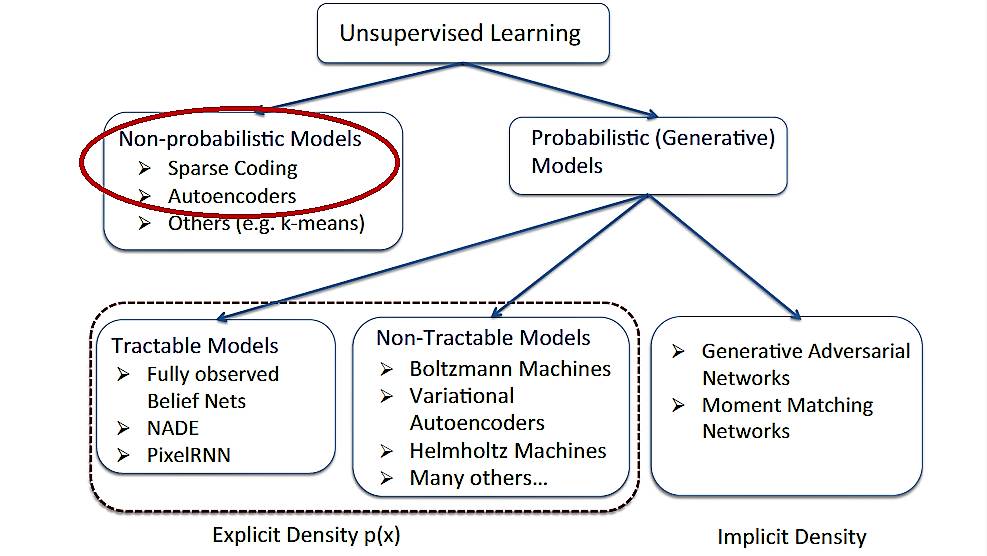
「无监督学习」（ ）现在已经成为深度学习领域的热点。和「有监督学习」相比，这种方法的最大优势就在于其无须给系统进行明确的标注（label）也能够进行学习。最近，在德国的图宾根，机器学习夏训营（   ）正在如火如荼地进行，其中来自 CMU 的   教授就带来了很多关于「无监督学习」的精彩内容。今天机器之心给大家分享的正是其课件中有关「无监督学习中的非概率模型」的相关内容，主要介绍了稀疏编码（ ）和自编码器（），这两种结构也是「无监督学习」的基本构件。完整课件可查看「阅读原文」PDF。

一、稀疏编码（ ）

1. 稀疏编码的概念

稀疏编码最早由  和 Field 于 1996 年提出，用于解释大脑中的初期视觉处理（比如边缘检测）。

目标：给定一组输入数据向量 { x1,x2,…,xN }，去学习一组基字典（ of bases）：

满足：

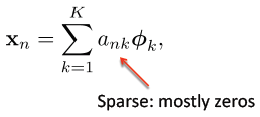
其中 ank 的值大部分都为 0，所以称为「稀疏」。每一个数据向量都由稀疏线性权值与基的组合形式来表达。

2. 稀疏编码的训练

为输入图像片段；

为要学习的基字典（ of bases）。

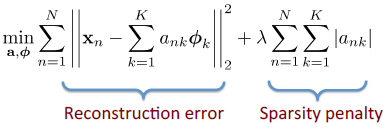
这个表达式的第一项为重构误差项；第二项为稀疏惩罚项。

交替性优化：

1. 固定基字典，求解激活值 a（这是一个标准的 Lasso 问题）；

2. 固定激活值 a，优化基字典（凸二次规划问题—— QP ）。

3. 稀疏编码的测试过程

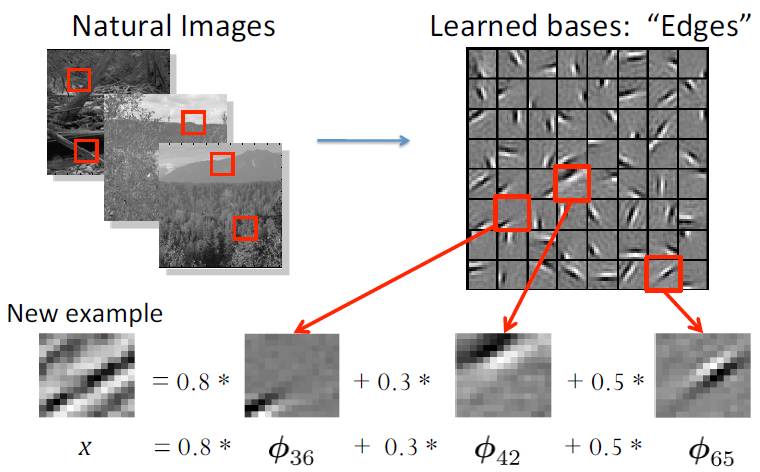
0, 0, …, 0.8, …, 0.3 …, 0.5, …

为系数矩阵，也叫做特征表示（ ）。

下图为应用稀疏编码进行图像分类的相关实验结果，该实验是在  物体类别数据集中完成的，并且用经典的 SVM 作为分类算法。

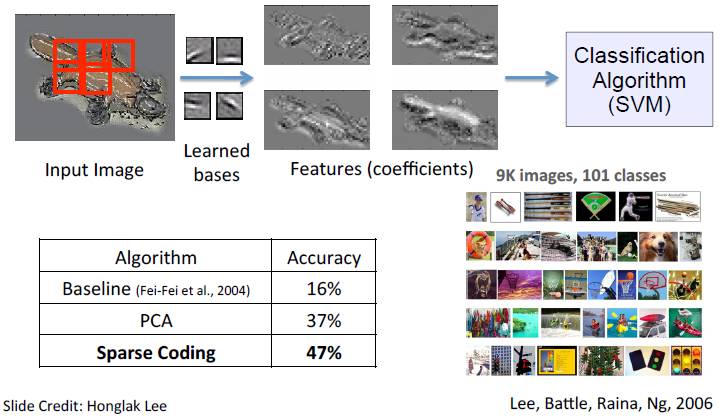
4. 稀疏编码的相关解释

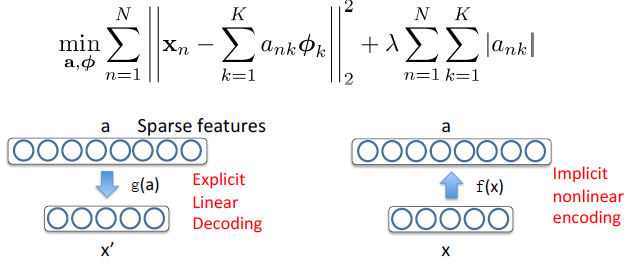
二、自编码器（）

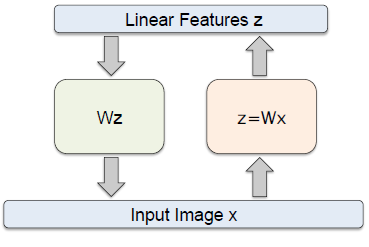
1. 自编码器结构

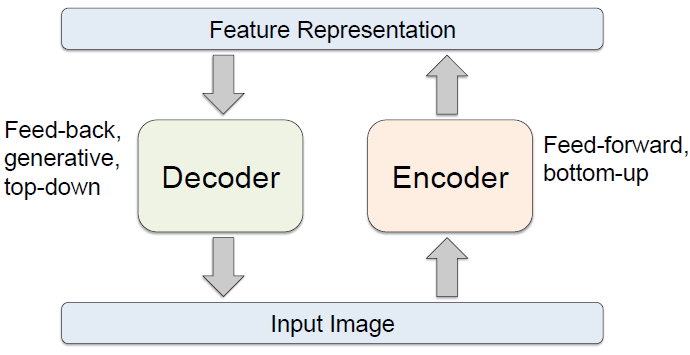
2. 自编码器范例

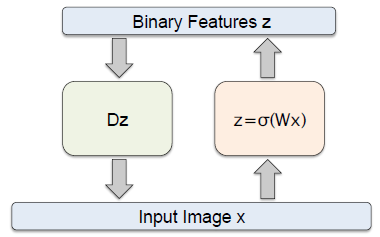
如上图所示，编码器的过滤器（）为 W，函数为  函数，

解码器的过滤器（）为 D , 函数为线性回归函数。

这是一个拥有 D 个输入和 D 个输出的自编码器，并且包括 K 个隐单元（ units）, K

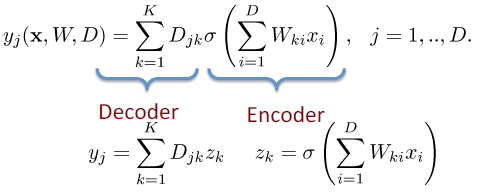
我们可以通过使重构误差（ error）最小化来决定网络的参数 W 和 D ：

3. 其它自编码模型

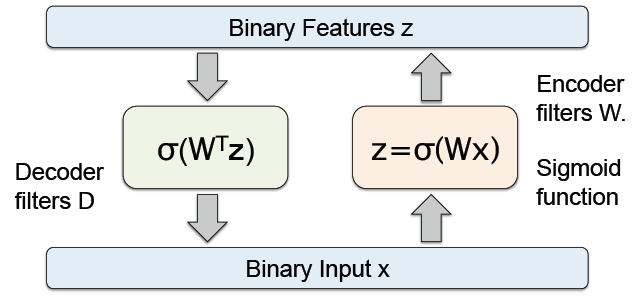
预测稀疏分解（  ）：

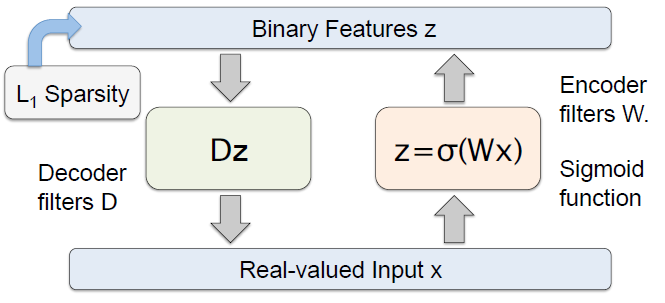
在训练过程中：

可以看到，这种结构在解码器部分加入了稀疏惩罚项（详见以上关于稀疏编码的内容）。

4. 堆叠式自编码器（ ）

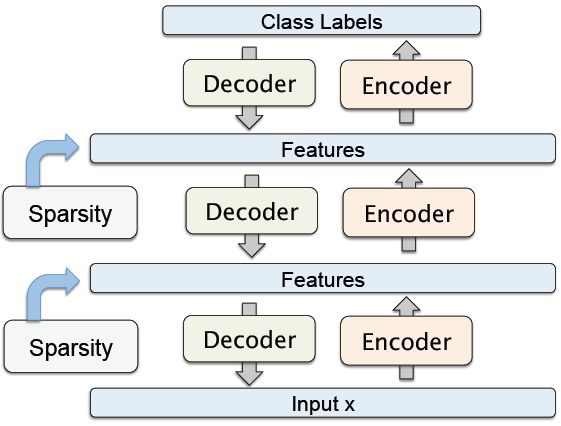
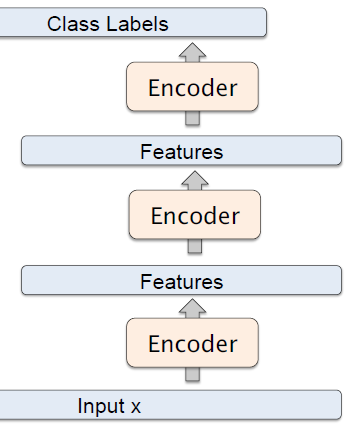
这是一种「贪婪」的分层学习。如果我们去掉解码器部分，并且只使用前馈部分，会发现这是一个标准的类似于卷积神经网络的结构，参考下图。可以使用反向传播来对参数进行调校。

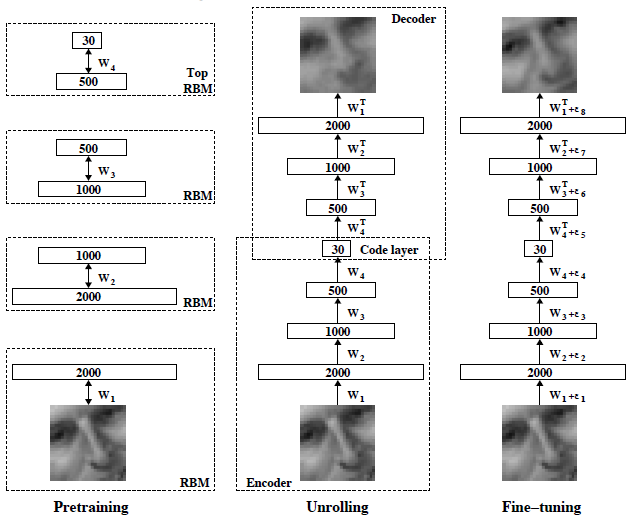
5. 深度自编码器结构及其相关实验结果