作者简介:热爱科研的仿真开发者,修心和技术同步精进,项目合作可私信。
个人主页:科研工作室
个人信条:格物致知。
更多完整代码及仿真定制内容点击
️ 内容介绍
在机器学习和人工智能领域,回归预测是一种重要的任务,它可以用来预测一个或多个连续变量的值。在本文中,我们将介绍一种基于粒子群优化门控循环单元(PSO-GRU)神经网络的回归预测方法。
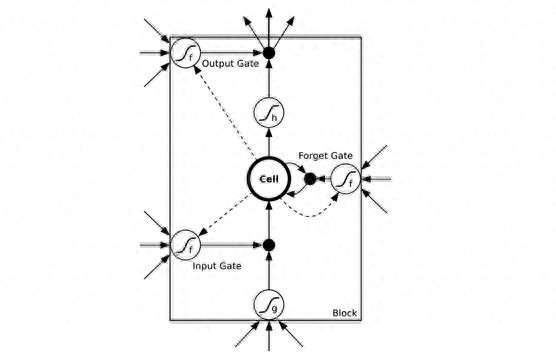
门控循环单元(GRU)是一种常用的循环神经网络(RNN)模型,它在序列建模任务中具有优秀的性能。然而,GRU模型的参数优化仍然是一个挑战,尤其是对于多输入单输出的回归预测问题。为了解决这个问题,我们引入了粒子群优化(PSO)算法来优化GRU模型的参数。
PSO算法是一种基于群体智能的优化算法,它模拟了鸟群觅食的行为。在PSO算法中,每个粒子代表一个候选解,它通过不断地调整自己的位置和速度来搜索最优解。在我们的方法中,每个粒子代表一个GRU模型的参数组合。
我们的PSO-GRU模型的训练过程如下:首先,我们初始化一群粒子,并随机生成它们的初始位置和速度。然后,对于每个粒子,我们根据其当前位置计算出对应的GRU模型,并使用训练数据进行训练。在训练过程中,我们使用均方误差(MSE)作为损失函数来衡量模型的性能。接下来,我们根据每个粒子的适应度评估其表现,并更新其速度和位置。最后,重复以上步骤直到满足停止准则。
通过使用PSO算法优化GRU模型的参数,我们可以提高回归预测的准确性。实验结果表明,我们的PSO-GRU模型在多个回归预测任务中取得了优于传统GRU模型的性能。这表明PSO算法可以有效地搜索GRU模型的参数空间,并找到最优解。
总结起来,我们在本文中介绍了一种基于粒子群优化门控循环单元(PSO-GRU)神经网络的回归预测方法。通过使用PSO算法优化GRU模型的参数,我们可以提高回归预测的准确性。我们的实验结果表明,PSO-GRU模型在多个回归预测任务中取得了优于传统GRU模型的性能。未来的研究可以进一步探索其他优化算法与循环神经网络的结合,以提高回归预测的性能。
核心代码
% This function initialize the first population of search agentsfunction Positions=initialization(SearchAgents_no,dim,ub,lb)Boundary_no= size(ub,2); % numnber of boundaries% If the boundaries of all variables are equal and user enter a signle% number for both ub and lbif Boundary_no==1Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;end% If each variable has a different lb and ubif Boundary_no>1for i=1:dimub_i=ub(i);lb_i=lb(i);Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;endend
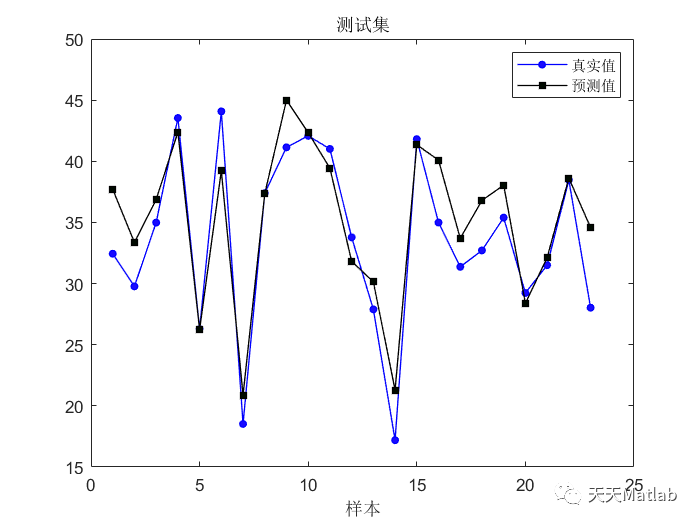
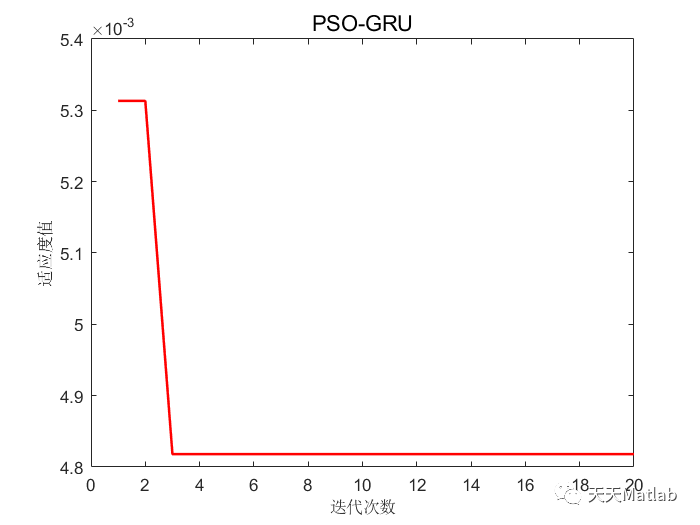
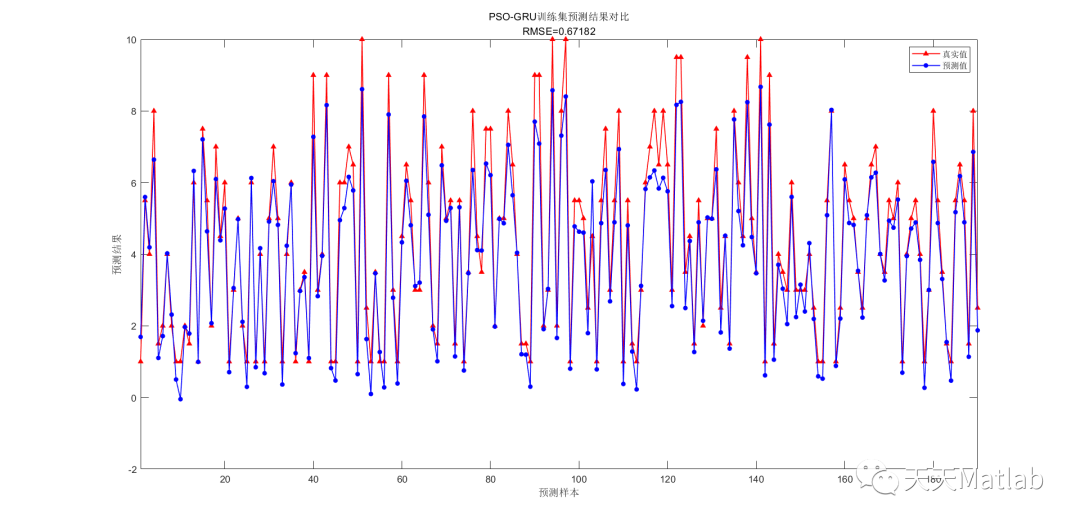
️ 运行结果
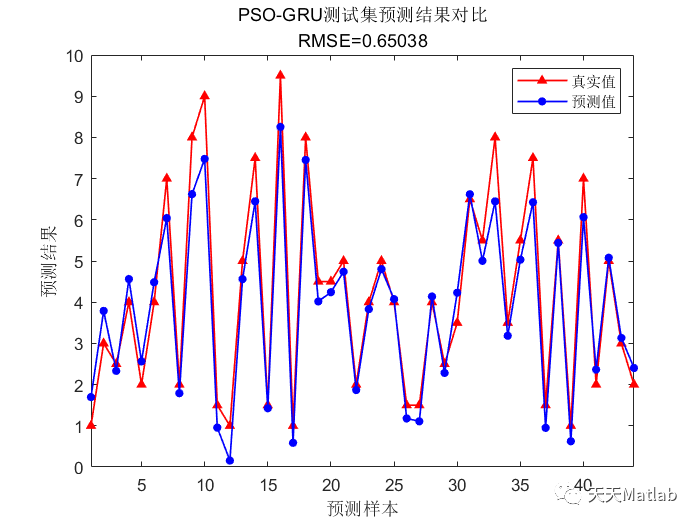
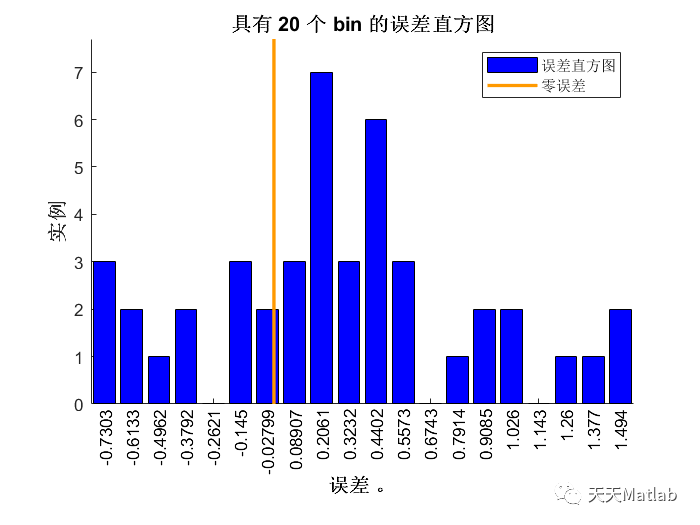
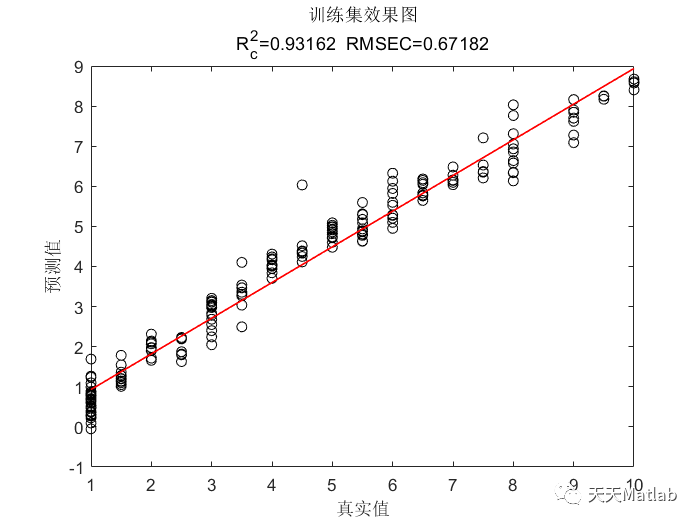
相关文章