召回率、精确率、准确率、F1值到底是什么？

从混淆矩阵理解

假定现在有一个猫狗识别程序，并且假定狗为正类别（）猫为负类别（）。程序在对12张狗和10张猫的混合图片进行识别后，判定其中8张图片为狗，14张图片为猫。

经人工核对在这8张程序判定为狗的图片中仅仅只有5张图片的确为狗，因此这5张图片就被称为预测正确的正样本（True , TP）；而余下的3张被称为预测错误的正样本（False , FP）。

经人工核对在14张被判定为猫的图片中仅有7张为真实的猫。即预测正确的负样本（True , TN)；而余下的7张被称为预测错误的负样本（False , FN）。

，根据这一识别结果，我们便可以得到如图1所示的混淆矩阵（ ）。

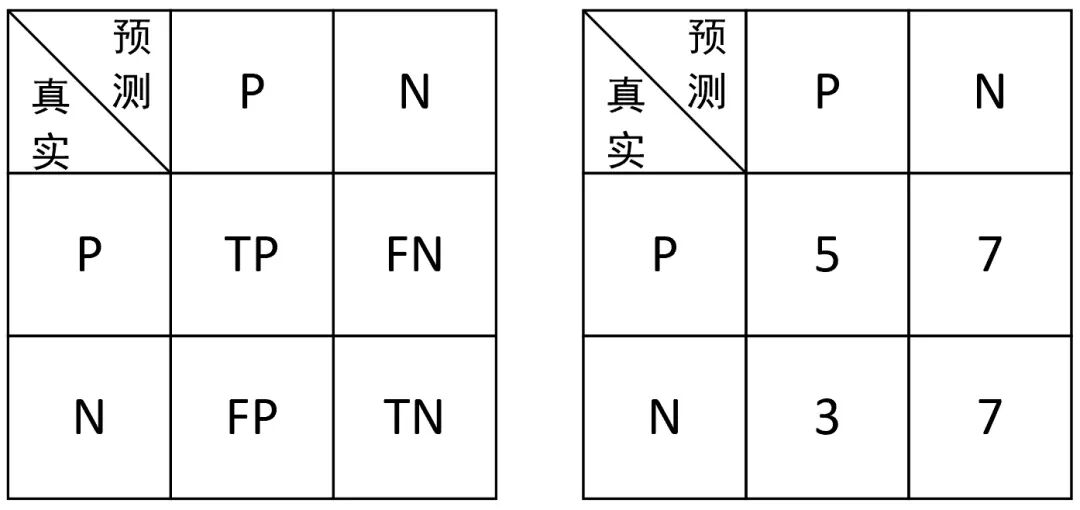
图 1. 混淆矩阵图

定义完上述4种分类情况后就能得出各种场景下的计算指标公式

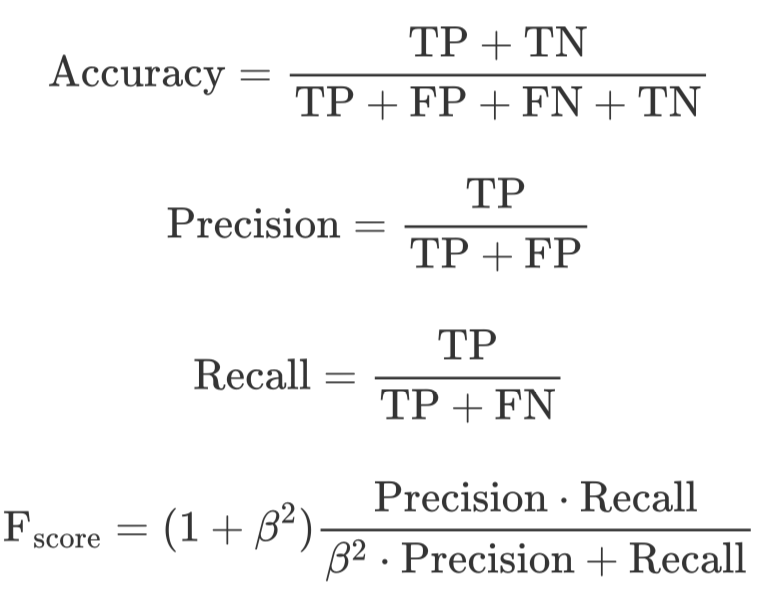
注意： 当中时称为值，同时也是用得最多的评价指标。

可以看到，精确率计算的是预测对的正样本在整个预测为正样本中的比重，而召回率计算的是预测对的正样本在整个真实正样本中的比重，因此一般来讲，召回率越高也就意味着这个模型寻找正样本的能力越强（例如在判断是否为癌细胞的时候，寻找正样本癌细胞的能力就十分重要），而则是精确率与召回率的调和平均。

从图示直观理解

根据精确率和召回率的定义，我们还可以通过更直观的图示来进行说明，如图2所示。

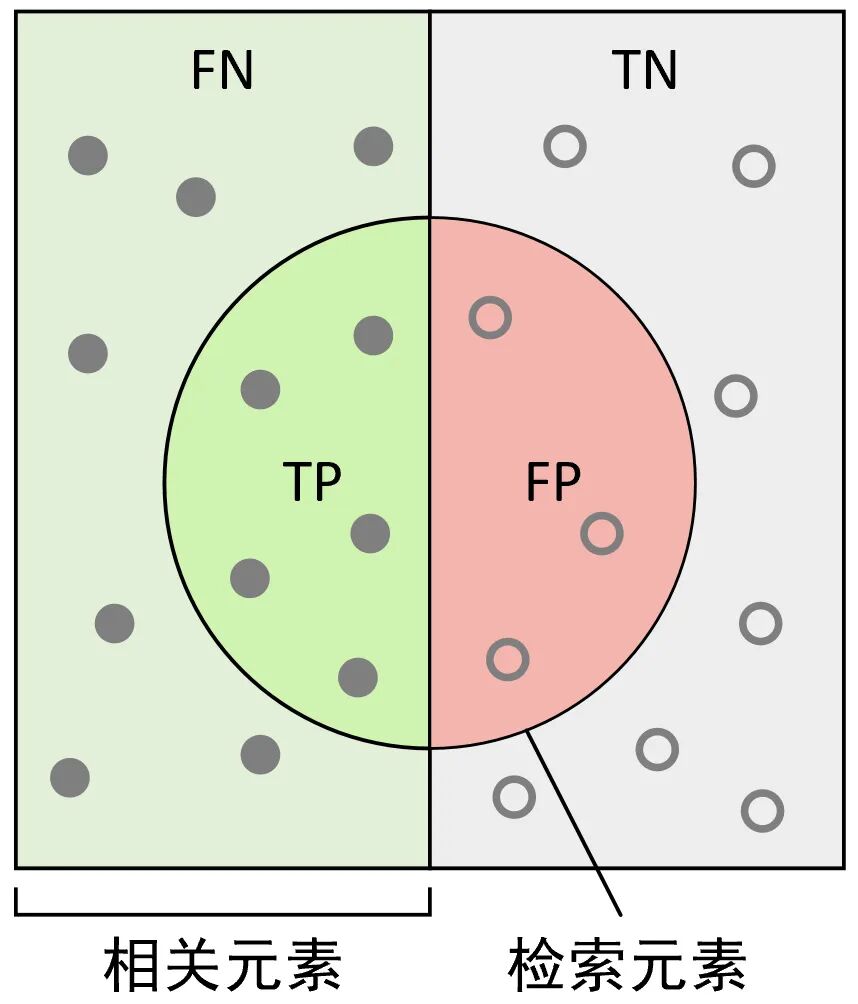
图 2. 分类情况分布图

在图2中，左侧的所有实心样本点为正样本（相关元素），右侧的所有空心点为负样本，中间的圆形区域为模型预测的正样本（检索元素），即圆形左侧为模型将正样本预测为正样本的情况，右侧为模型将负样本预测为正样本的情况。例如现在可以想象这么一个场景，某一次我们在使用搜索引擎搜索相关内容（正样本）时，搜索引擎一共检索返回了30个搜索页面（搜索引擎认为的正样本），而搜索引擎返回的结果就相当于是图2中对应的圆形区域，所以精确率和召回率还可以通过图3来形象地进行表示。

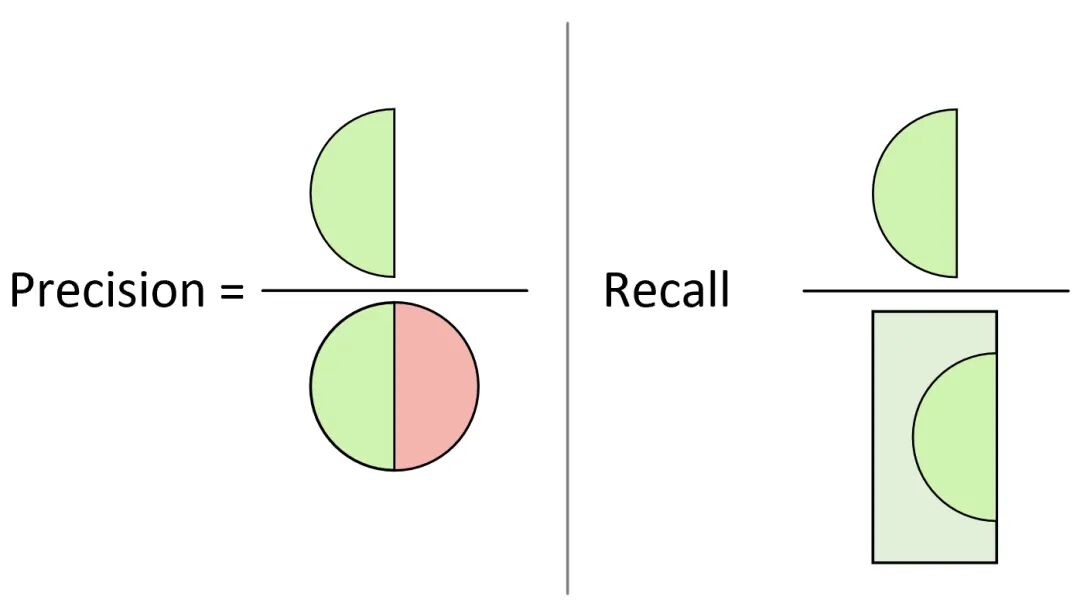
图 3. 精确率召回率图示

从图3中更能直观地看出，精确率计算的是预测正确的正样本在整个被预测为正样本中的占比；而召回率计算的是预测正确的正样本在所有真实正样本中的占比。

扫码订阅专栏永久畅读所有文章，

往期精选推荐

点击下图购买掌柜编著新书