收敛性：依分布收敛

最近在复习（预习）概率论收敛性的专题，学到自闭，看完就忘啥也记不住，就想着系统地整理一下，先从最弱

的依分布收敛开始。

啥是依分布收敛？

随机变量序列{Xn}有分布函数列{Fn(x)}，随机变量X有分布函数F(x)，若在F(x)的任意连续点上

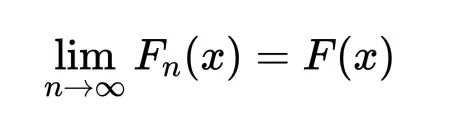
成立，则称Fn(x)弱收敛于F(x)，或Xn依分布收敛于X，分别记作

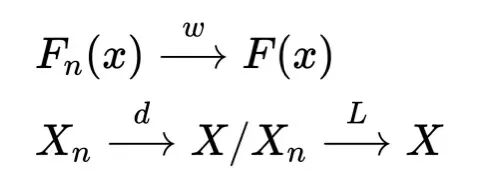
w表示，即弱收敛；

d表示，查了一下L是Law的意思，在一些古早的经典教材中随机变量的分布也叫随机变量的Law，后来为了和大数定律中的Law区别才有了的说法。

有俩注意事项：

(1)依分布收敛要满足在F(x)的连续点成立，它不是点点收敛。（据说依分布收敛的概念在夏令营面试和考研复试会经常被问到，老师会特别在意答案里有没有“连续点”这个关键词。）

举个栗子

单点分布P(Xn=1/n)=1

分布函数

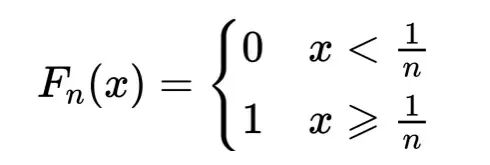
n→∞时

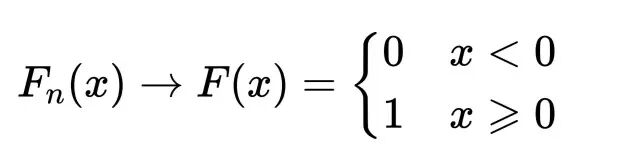
Xn依分布收敛于X，P(X=0)=1（也可以说是Xn依分布收敛到0）

但是在F(x)的间断点0处Fn(x)并没有收敛到F(x),因为Fn(x)=0，F(x)=1

(2)只有{Fn(x)}收敛到一个分布函数时，才是依分布收敛。

再举个栗子

P(Xn=n)=1

分布函数

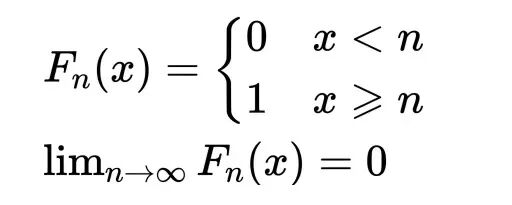
n→∞时Fn(x)不满足分布函数的性质，故Fn(x)不收敛到一个分布函数，不是依分布收敛。

来两个例题：

eg1：（2016-清华432）

第一问比较简单，Xn服从两点分布，直接写出分布函数就行了，第二问等以后专门讲矩收敛的时候再看。

Xn的分布列：

Xn

1-1/n

1/n

Xn分布函数：

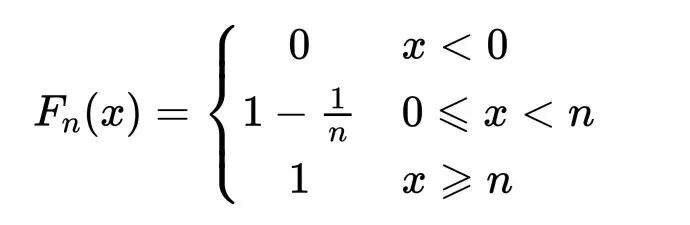
n→∞时

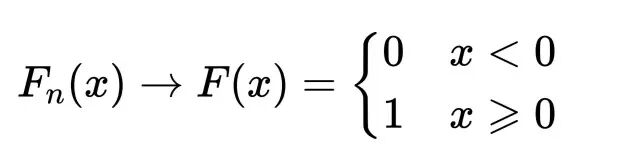
所以Xn的分布函数收敛。

eg2：（2017-清华432）

只看第二问（不要在意总分的细节）

先求次序统计量x(n)的分布，再求左边那一坨的分布函数。

①直接用次序统计量的公式求x(n)的分布

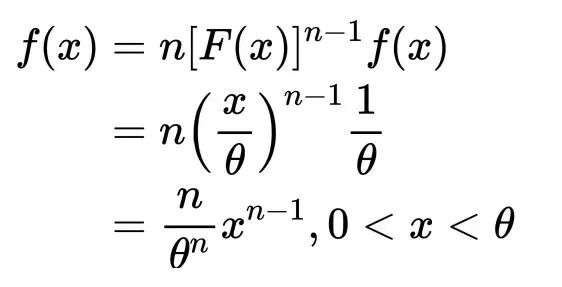
②令左边那一坨等于Y，求Y的分布函数，这里有两种方法，一个是先用公式法求出Y的pdf，再积分求分布函数，既然最后要求Y的分布函数，定义法直接求分母函数会省很多步骤。

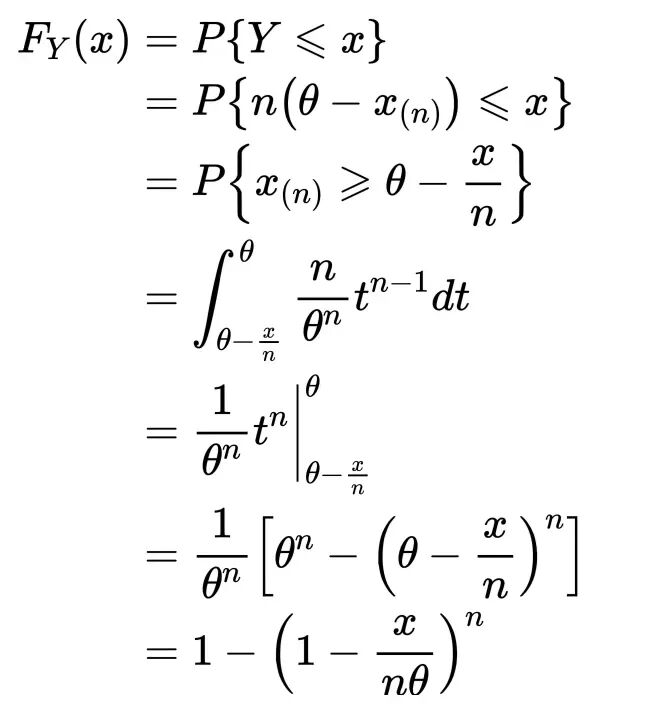
③n→∞，求Y的极限分布，即X的分布

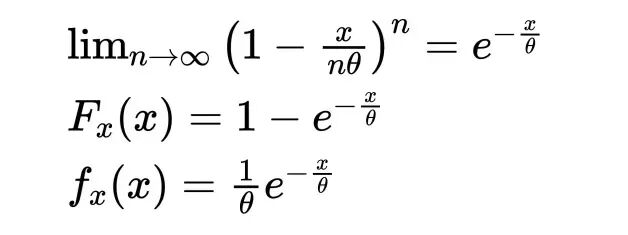
故X服从参数为1/θ的指数分布，即X~Exp(1/θ)

下次讲依概率收敛。