【关于 正则化】那些你不知道的事

个人笔记：

一、L0，L1，L2正则化 篇1.1 正则化 是什么？

我们所说的正则化，就是在原来的loss 的基础上，加上了一些正则化项或者称为模型复杂度惩罚项。

1.2 什么是 L0 正则化 ？

就像一个法官判决，你偷了一毛钱，他杀了一个人，法官均以“价值观不正确”为由，把你们判一样的罪……只有一点都没参与的人，才不会被判刑。

1.3 什么是 L1 （稀疏规则算子 Lasso ）正则化 ？

∑j=1m|θj|

拿法官举例子，就是，法官要按照你们的罪行量刑判罪，但是都得判，无论你影响最终是好是坏（比如你杀了个人，这个人也是个坏人，但是你还是犯了杀人罪得判刑）都按照罪行判罪。于是就都取个绝对值，表示都判，然后按照罪行大小判罪了……

参数稀疏 的 优点：

1.4 什么是 L2 正则化（岭回归 Ridge 或者 权重衰减 Decay）正则化 ？

∑j=1mθj2

二、对比篇2.1 什么是结构风险最小化？

在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，以此提高泛化预测精度。

下面是一个图像解释（假设X为一个二维样本，那么要求解参数w也是二维)：

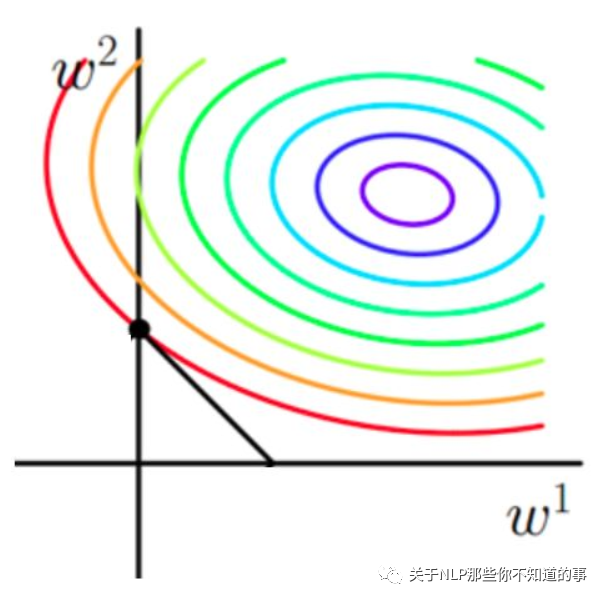
2.2 从结构风险最小化的角度理解L1和L2正则化

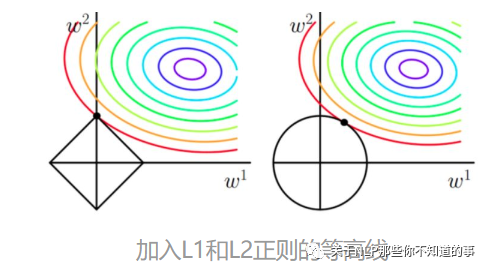
从上面两幅图中我们可以看出：

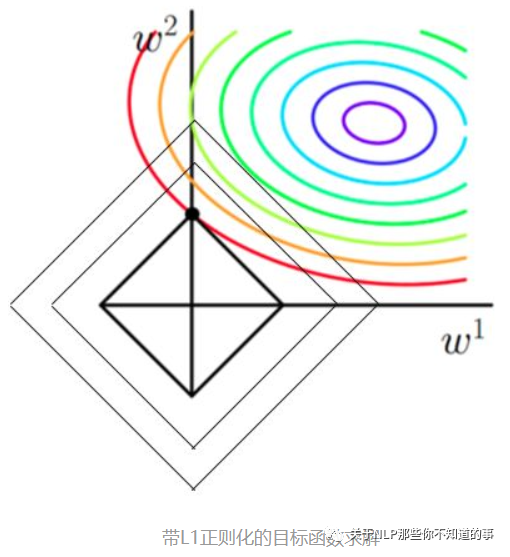
以同一条原曲线目标等高线来说，现在以最外圈的红色等高线为例，我们看到，对于红色曲线上的每个点都可以做一个菱形，根据上图可知，当这个菱形与某条等高线相切（仅有一个交点）的时候，这个菱形最小。用公式说这个时候能使得在相同的1/N∗∑i=1N(yi−ωTxi)2下，由于相切的时候的C∥ω∥1，即|ω1|+|ω2|小，所以：能够使得1/N∗∑i=1N(yi−ωTxi)2+C∥ω∥1更小。

有了上述说明，我们可以看出，最终加入L1范数得到的解，一定是某个菱形和某条原函数等高线的切点。现在有个比较重要的结论来了，我们经过观察可以看到，几乎对于很多原函数等高曲线，和某个菱形相交的时候及其容易相交在坐标轴（比如上图），也就是说最终的结果，解的某些维度及其容易是0，比如上图最终解是

ω=(0,x)

这也就是我们所说的L1更容易得到稀疏解（解向量中0比较多）的原因。

当然了，光看着图说，L1的菱形更容易和等高线相交在坐标轴，一点都没说服力，只是个感性的认识，不过不要紧，其实是很严谨的，我们直接用求导来证明，具体的证明这里有一个很好的答案了，简而言之就是假设现在我们是一维的情况下

h(ω)=f(ω)+C|ω|

其中h(ω)是目标函数，f(ω)是没加L1正则化的目标函数，C|ω|是L1正则项，那么要使得0点成为最值的可能得点，，虽然在0点不可导，但是我们只需要让0点左右的导数异号，即

h左′(0)∗h右′(0)=(f′(0)+C)(f′(0)−C)